 Natürliche Zahlen ... Natürliche Zahlen ... |
| | Natürliche Zahlen sind ganzzahlige positive Zahlen.
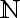 = {1;2;3;4;5;6;7;...} = {1;2;3;4;5;6;7;...}
0 gehört nicht zur Menge der natürlichen Zahlen.
Das Symbol für natürliche Zahlen ohne Null ist: 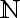 (Duden) oder (Duden) oder 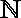 (DIN5473) (DIN5473)
Jede Zahl außer 1 hat einen Vorgänger -1. Jede Zahl hat einen Nachfolger +1.
Natürliche Zahlen mit 0 schreibt man 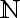 0 = {0;1;2;3;4;5;6;7;...} 0 = {0;1;2;3;4;5;6;7;...} |
 Gerade natürliche Zahlen ... Gerade natürliche Zahlen ... |
| | Vielfaches der Zahl 2. Eine Zahl ist ohne Rest durch 2 teilbar.
=> 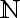 = {2;4;6;8;10;12;14;16;...} = {2;4;6;8;10;12;14;16;...} |
 Ungerade natürliche Zahlen ... Ungerade natürliche Zahlen ... |
| | Kein Vielfaches der Zahl 2. Eine Zahl ist ohne Rest nicht durch 2 teilbar.
=> 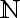 = {1;3;5;7;9;11;13;15;...} = {1;3;5;7;9;11;13;15;...} |
 Zehnersystem oder Dezimalsystem (lat. decem = zehn) oder Denärsystem ..., ... Zehnersystem oder Dezimalsystem (lat. decem = zehn) oder Denärsystem ..., ... |
| | Das Zehnersystem ist ein Stellenwertsystem mit der Basis 10.
=> Es gibt somit 10 Grundzahlen 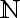 0 = {0;1;2;3;4;5;6;7;8;9} 0 = {0;1;2;3;4;5;6;7;8;9} |
 Zweiersystem oder Dualsystem (lat. dualis = zwei) oder Binärsystem ..., ... Zweiersystem oder Dualsystem (lat. dualis = zwei) oder Binärsystem ..., ... |
| | Das Zweiersystem ist ein Stellenwertsystem mit der Basis 2.
=> Es gibt somit 2 Grundzahlen 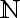 0 = {0;1} 0 = {0;1} |
 Primzahlen ... Primzahlen ... |
| | Natürliche Zahlen die genau zwei Teiler besitzen (1 und sich selber). 1 ist dabei keine Primzahl.
=> 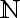 = {2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59;61;67;71;73;79;83;89;97;...} = {2;3;5;7;11;13;17;19;23;29;31;37;41;43;47;53;59;61;67;71;73;79;83;89;97;...}
Kleiner Trick beim Prüfen ob eine Zahl eine Primzahl:
» Gesuchte Zahl (Bsp. 71) nächste Quadratzahl ermitteln (Bsp. 9 denn 9*9=81, 81>71).
» Gesuchte Zahl (Bsp. 71) durch erste Primzahlen teilen (Bsp. 2 = geht nicht ergibt ein Rest).
» Gesuchte Zahl (Bsp. 71) durch nächste Primzahlen teilen (Bsp. 3 = geht nicht ergibt ein Rest).
Das ganze nun bis zur ermittelten Quadratzahl (Bsp. 9)
» Gesuchte Zahl (Bsp. 71) durch nächste Primzahlen teilen (Bsp. 5 = geht nicht ergibt ein Rest).
» Gesuchte Zahl (Bsp. 71) durch nächste Primzahlen teilen (Bsp. 7 = geht nicht ergibt ein Rest).
» In unserem Beispiel (71) muss durch 11 nicht mehr geteilt werden, da 11 größer ist als 9 ist.
Somit ist das Beispiel (71) eine Primzahl!
» Ergibt sich vorher beim Teilen kein Rest ist es auch keine Primzahl
(Bsp. 69:3 = 33 somit ist 69 keine Primzahl) |
 Quadratzahlen ... Quadratzahlen ... |
| | Zahlen, die sich ergeben, wenn man natürliche Zahlen mit sich selbst multipliziert.
=> 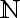 = {1;4;9;16;25;36;49;64;81;...} = {1;4;9;16;25;36;49;64;81;...} |
 Dreieckszahlen ... Dreieckszahlen ... |
| | Dreieckszahlen sind die Zahl 1 sowie die Zahlen, die sich nacheinander ergeben, wenn man zur Zahl 1 die Zahl 2 addiert, dann zum Ergebnis 3, dann zum Ergebnis 4 usw.
=> 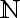 = {1;3;6;10;15;21;28;36;45;;55...} = {1;3;6;10;15;21;28;36;45;;55...} |
 Diagramm ... Diagramm ... |
| | Tabellen und Diagramme dienen der Zusammenfassung und Veranschaulichung von Zahlen, vor allem, wenn man größere Zahlenmengen besser überblicken will. Bestimmte Informationen können dadurch besser abgelesen werden. |



















































